强扩展(Strong Scaling)是衡量对于固定的总体问题大小,求解问题时间如何随着系统中添加的处理器的增加而缩短的量度。表现出线性强扩展的代码的加速比等于使用的处理器数量。
Strong Scaling 通常等同于阿姆达尔定律(Amdahl's Law),该定律指定了并行化串行代码的各个部分可以预期的最大加速比。本质上讲,它定义了程序的最大加速比 S:
$$S = \frac{1}{(1-P)+\frac{P}{N}}$$
其中,P 是可以并行化的代码占总耗时的比例,N 是代码的并行部分运行的处理器数。N 越大(即处理器数量越多),P/N 分数越小。将 N 视为一个非常大,可以将上面公式转换为 $S=\frac{1}{1-P}$ 。现在,如果串行程序中的 3/4 运行时间是可以并行化的,则该串行代码的最大加速比为 1 / (1 - 3/4) = 4.
在大多数情况下,P 的可并行化部分占比越大,潜在的加速就越大。
弱扩展(Weak Scaling)是衡量求解时间随着系统中处理器的增加如何变化的指标,假设每个处理器能解决的问题大小固定(处理的数据规模),总体问题大小随着处理器数量的增加而增加。
Weak Scaling 通常等同于 Gustafson 定律,该定律指出,在实践中,问题大小随着处理器的数量而变化。因此,程序的最大加速比 S 为:
$$S = N + (1-P)(1-N)$$
其中,P 是可以并行化的代码部分时间占比,N 是代码的并行部分运行的处理器数量。
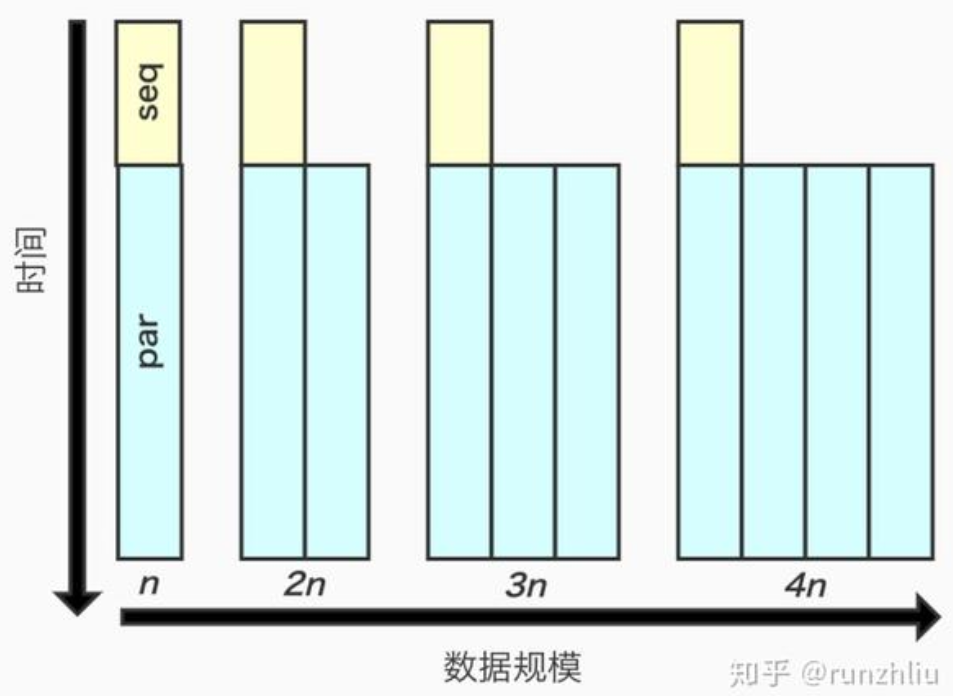
看待 Gustafson 定律的另一种方式是,在我们扩大系统规模时,执行时间是保持变的,问题的大小随着处理器数量而增加。请注意,Gustafson 定律假设串行执行与并行执行代码的比例保持不变。如下图:
其中,黄色是顺序执行代码,蓝色是可并发执行代码。随着问题规模扩展,数据规模扩大,可以通过增加并行部分代码的处理器数量(条形数量是指处理器,随着数据规模增大),来使整个代码执行时间不变。
Amdahl 定律表明,在某个数据规模的问题下,提升系统中某个部分代码的性能,对整个系统的性能提升上限。
Gustafson 定律表明,在整个系统执行时间不变下,可以通过增加执行并行部分代码的处理器数量,使系统处理的问题规模变大。
参考: https://docs.nvidia.com/cuda/cuda-c-best-practices-guide/#application-profiling